GPS定位卫星受摄轨道根数

显然,该方程与前面无摄运动方程(3-17)是不一样的。通过无摄运动方程,可以解 得卫星的坐标(x, y, z) T 和速度( x& , y& , z&) T ,并用一组轨道根数as、es、Ω、i、ωs 和t0 来 表示。而按照方程(3-28)求得的卫星受摄运动轨道的轨道根数则不再保持常数,它们是时 间的函数。假设在观测历元t 时刻,解得轨道根数为as(t)、es(t)、Ω(t)、i(t)、ωs(t) 和τ0(t),则这一组轨道根数称为观测历元t 的受摄轨道根数。假如在观测历元t 这个瞬间, 摄动力突然全部消失,则卫星将沿着这一瞬间的受摄轨道根数所决定的开普勒椭圆作圆周运 动,所以受摄轨道根数也叫瞬时轨道根数(Instantaneous Orbital Elements),或密切轨道根数 (Osculating Orbital Elements)。
在方程(3-29)中,K s是所有摄动力加速度之和。如果引入符号: E &r& 为非球形引力摄动加速度(Acceleration Due to the Non-spherically and Inhomogeneous Mass Distribution within the Earth); S r&& 、M &r& 为日、月引力摄动加速度(Accelerations Due to the Sun and the Moon); SP &r& 、&r&A为太阳光压、地球反射光压(Accelerations Due to Direct and Earth-reflected Solar Radiation Pressure); e &r&、 o &r& 为固体潮和海潮摄动加速度(Accelerations Due to Earth and Oceanic Tides); D &r& 为大气阻力摄动加速度(Acceleration Due to the Atmospheric Drag)。 如图3-7 所示,即有:
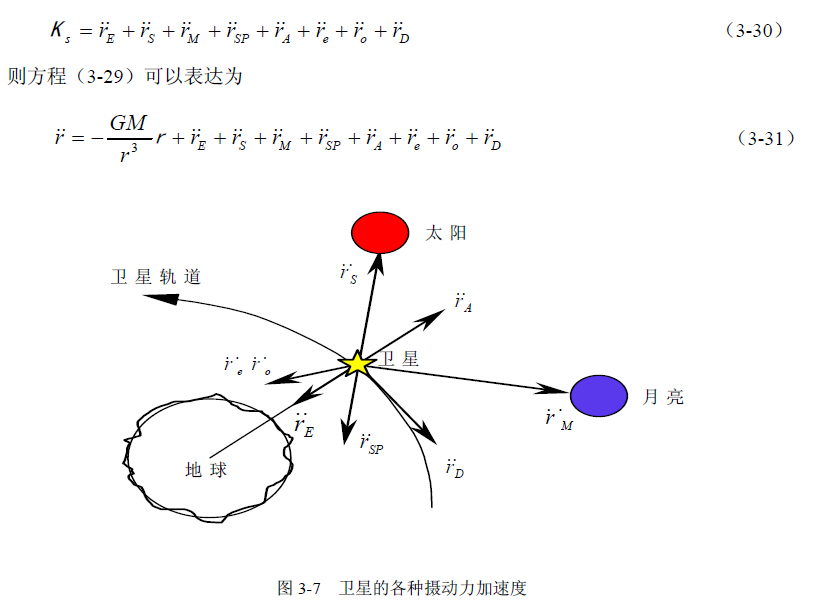
总的说来,摄动力可以分为两类:保守力(Conservative Force)和耗散力(Dissipative Force)。前者可以用位函数来表示受摄运动方程,比如非球形引力和日月引力;后者不宜用 位函数表示,而只能用摄动力表示受摄运动方程,比如潮汐力、大气阻力和太阳光压。理论 分析表明,GPS 卫星作为高轨卫星,对大气阻力、潮汐力(包括海潮、固体潮和大气潮)、 地球反射光压以及非球形引力位展开式的高阶项并不敏感。如果将它们忽略不计,则方程 (3-31)可以进一步简化为:
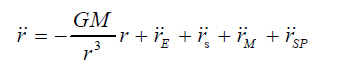
(文章编辑:锐峰汇智GPS定位器 https://www.rfgsm.com/)
尊敬的访客:如果您想了解或购买GPS定位 防盗产品,请点击下方按钮联系我们


您也可以直接拨打客服热线:4007-888-200
推荐阅读:
GPS应用于大型设备的超精密安装
GPS定位技术在精密工程测量中的应用
GPS定位技术在普通工程测量中的应用
GPS技术在工程测量中的应用
GPS定位在大地(控制)测量方面的应用



