GPS卫星的无摄运动

　　中心引力是匀质球体形成的理想的引力作用，因此无摄轨道的数字特征可以精确获得， 该理想轨道是分析卫星运动的基础。

　　开普勒定律包含三条定律，是德国天文学家开普勒(Johannes Kepler)(1571～1630)提 出的，主要用来描述行星绕太阳运动的基本规律。该定律同样适合用来描述卫星绕地球运动 的基本规律。

　　行星绕太阳运行轨道是一个椭圆，太阳位于该椭圆的一个焦点上。

　　这一定律说明，在中心引力作用下，卫星的无摄轨道(和行星轨道一样)，也是一个椭 圆。这个椭圆叫开普勒椭圆(Kepler Ellipse)，地球质心位于该椭圆的一个焦点上。如图 3-1 所示，卫星离地球质心最远一点称为远地点(Apogee)，最近一点称为近地点(Perigee)。

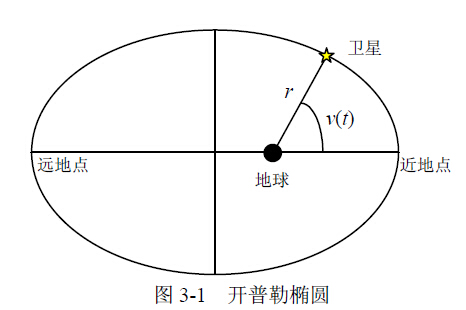
　　设r 为卫星到地心的距离(向径)，as 为开普勒椭圆长半轴，es 为椭圆偏心率，v(t)为 卫星真近点角，则卫星绕地球质心运动的无摄轨道方程为:

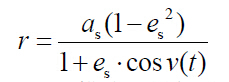
　　其中v(t)描述卫星相对于近地点位置，它是时间的函数(该方程的由来请参见本章3.2.3)。

　　行星围绕太阳运行时，行星与太阳的连线(向径)在相同的时间内扫过相同的面积。和行星一样，在轨道上运行的卫星也同时具有势能和动能，其中势能的大小取决于卫星在地 球引力场中的位置，动能是卫星运动速度的函数。根据能量守恒定理，在近地点时，卫星势 能达到最大，这时动能最小，速度也最小。而在远地点时情况则正好相反。以地球绕太阳公 转为例，地球运行至近日点时(1 月3 日左右)，速度达到最快，日速约1°01′9.9″。在远日 点时(7 月4 日左右)，速度达到最慢，日速约0°57′11.5″。

　　假设ms 和vs 分别是卫星的质量和速度，M 为地球质量，G 为引力常数，则卫星的势能 与动能之和理论上应该保持不便，即:

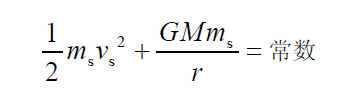
　　如图3-2 所示，开普勒第二定律说明，卫星的运行速度并非常数，而是不断变化的。在近地 点时的速度最大，远地点的速度则最小。开普勒第二定律也叫面积定律(The Law of Areas)



（编辑整理：锐峰汇智https://www.rfgsm.com/）

尊敬的访客：如果您想了解或购买GPS定位 防盗产品，请点击下方按钮联系我们

您也可以直接拨打客服热线：4007-888-200

推荐阅读：
GPS应用于大型设备的超精密安装
GPS定位技术在精密工程测量中的应用
GPS定位技术在普通工程测量中的应用
GPS技术在工程测量中的应用
GPS定位在大地(控制)测量方面的应用